Accelerate Convolution with Img2Col

Recall convolution operation, where we add each element of the feature matrix to its local neighbours, weighted by the kernel. An illustration is at this webpage.

As one can immediately notice, as the kernel “slides” through the feature matrix, same feature matrix elements are repeatedly accessed, thus would cause frequent cache misses. Transforming image convolution to GEMM (General Matrix Multiply) alleviates this problem, while taking advantage of the linear algebra library, or the acceleration provided by the domain specific architecture.

Algorithm

The algorithm can be described with a single image below - (image source). The top sub-figure presents a traditional convolution operation, where both the input feature and the convolution kernel consists of 3 channels, while the bottom sub-figure presents the transformed matrix mulitplication operation. Below sections illustrates the algorithm with the image.

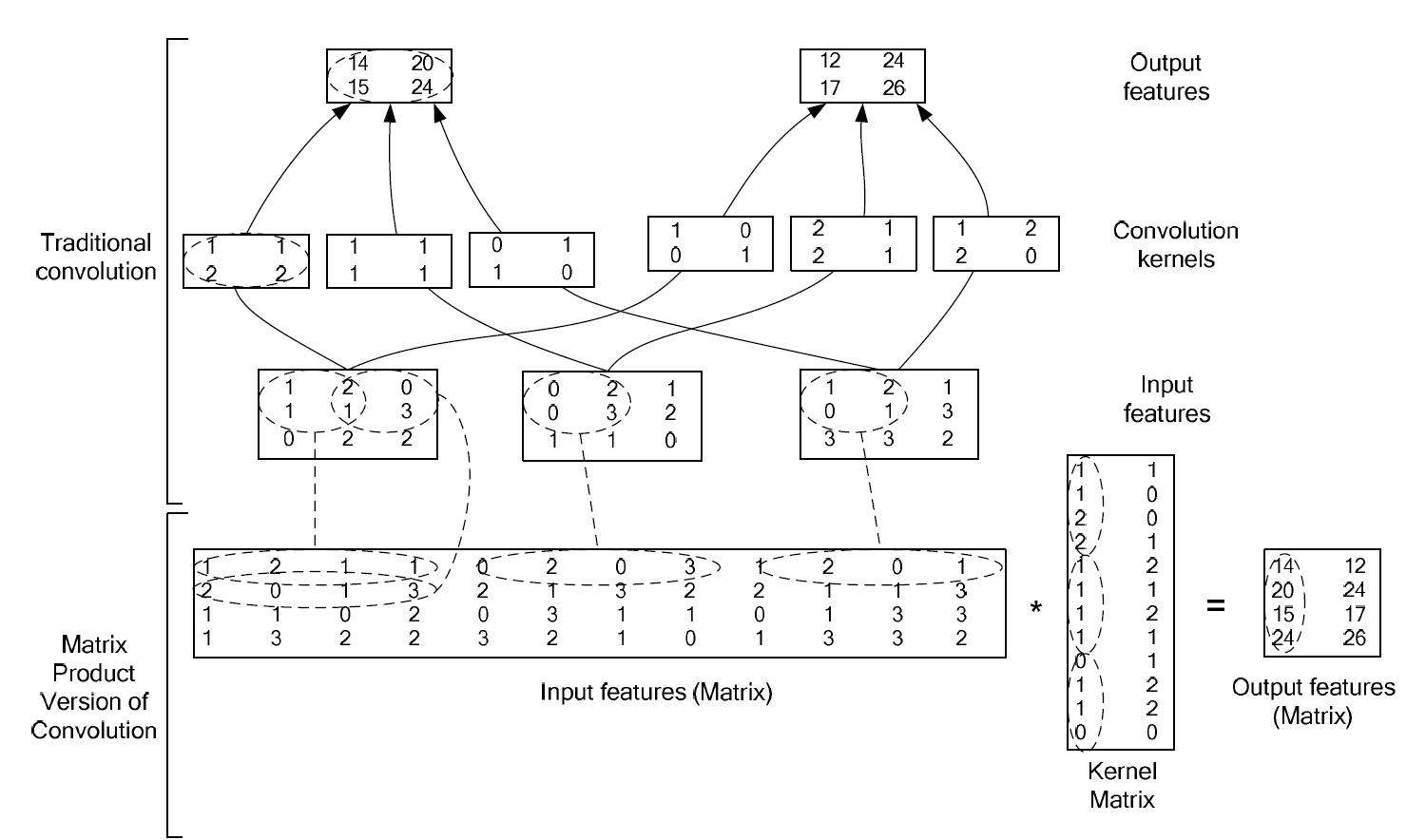
Transform Input Feature to Input Matrix

The first step is transforming input feature to matrix.

Take the example of the left-most input channel of size 3x3. Each step as the kernel “slides” through the input channel, a 2x2 input sub-matrix is exposed to the kernel, and we flatten the input sub-matrix (in NZ data format) to a row vector of size 1x4. Concatenate the transformed row vectors as the input matrix of one channel, of size 4x4. For an input with multiple channels, the img2col transformation is applied to each channel individually first. Then, the resulting matrices are concatenated horizontally. For example, applying img2col to each of the three 3x3 input channels results in three separate 4x4 matrices. Concatenating these three matrices side-by-side produces the final input matrix of size 4x12.

Transform Convolution Kernel to Kernel Matirx

The second step is transforming the convolution kernel to kernel matrix.

Take the example of the left-most convolution kernel of size 2x2. We flatten the convolution kernel (in NZ data format) to a of size 4⨉1. For more than one channel, concatenate the transformed column vectors as the kernel matrix of one kernel, of size 12x1. For more than one kernel, each kernel is flattened into a column vector and these vectors are concatenated horizontally (side-by-side). For example, the first 3-channel kernel (size 2x2x3) is flattened into a 12x1 column vector. The second kernel is also flattened into a 12x1 vector. Placing these two vectors side-by-side forms the final kernel matrix of size 12x2.

Output Matrix = Input Matrix * Kernel Matirx

The resulting output matrix has a size of 4x2. To transform this back into the final output feature map, each column of the output matrix must be reshaped. The first column (a 4x1 vector) is reshaped into a 2x2 matrix, forming the first output channel. The second column is likewise reshaped into a 2x2 matrix to form the second output channel.